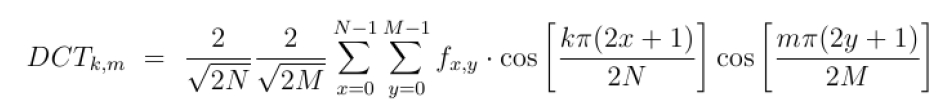In dieser Übung wird der Informationsgehalt eines Bildes reduziert und die Auswirkung auf die Interpretierbarkeit für den Menschen betrachtet. Die Reduzierung der Informationen kann für eine Komprimierung verwendet.

Wenden Sie die folgenden Aufgaben auf die Bilder data/yellowlilly.jpg und data/cameraman.png an.

Aufgabe a) Entfernen hochfrequenter Frequenzen

Implementieren sie die Funktion und remove_dft(img, rate), wobei mit der diskreten Kosinus- bzw. Fouriertransformation folgende Schritte durchgeführt werden sollen:

Iterieren Sie Blockweise über das Bild mithilfe zweier for-Schleifen und einer Blockgröße von 8x8 Pixel
Verwenden Sie np.fft.fft2() um den Block in den Frequenzraum zu transformieren
Entfernen Sie die n hochfrequentesten Koefizienten mit n = 8 * 8 * rate
Transformieren Sie den Block zurück in den Ortsraum mit np.fft.ifft2

Wie stark wirkt sich der Parameter rate auf die Interpretierbarkeit des Bildes für den Menschen aus?

Die Lösung ist in der Date l_a.py zu finden.

Aufgabe b) Diskrete Kosinus Transformation

Implementieren Sie eine Funktion dct(a: np.ndarray), welche als input eine zweidimensionale Matrix erhält und auf diese die 2D Diskrete Kosinus Transformation nach

anwendet und ausgibt.

Validieren Sie Ihre Funktion, indem Sie die fft2() und ifft2() Funktion aus Aufgabe a) durch die dct() und idct() Funktionen ersetzen. Die inverse der Transformation ist mit der Funktion idct(a: np.ndarray) gegeben, welche bereits in l_b.py implementiert ist.

Aufgabe c) Fragen

Wie kann die Reduzierung der Fourier-Koeffizienten für eine Komprimierung genutzt werden?
Was versteht man unter diskreter Kosinustransformation und was ist der wesentliche Unterschied zur DFT?
Welchen Vorteil bietet die DCT gegenüber der FFT in der Praxis?